Приближенные комбинированные методы нахождения кратчайшего маршрута
Применив три метода , , расчета базового маршрута и комбинированный метод их улучшения, получили три приближенных метода расчета маршрута:
метод 3.1: procedure GreedilyCorrect(N: Integer; var G: TIntVec; var Path: Integer); begin Greedily(N,G); CorrectPath(N,G,Path); end;
метод 3.2: procedure WoodyCorrect(N: Integer; var G: TIntVec; var Path: Integer); begin Woody(N,G); CorrectPath(N,G,Path); end;
и метод 3.3: procedure SimplyCorrect(N: Integer; var G: TIntVec; var Path: Integer); begin Simply(N,G); CorrectPath(N,G,Path); end;
В экспериментах с методами 3.1–3.3 установлено, что ни один из них не является предпочтительным. В зависимости от матрицы А лучший результат с равной вероятностью мог дать любой из этих методов (интересно, что даже простейший базовый маршрут G[i] = i после улучшений нередко трансформировался в самый короткий маршрут, что свидетельствует о том, что решение задачи практически не зависит от выбора базового маршрута). Поэтому в качестве рабочего применяли комбинированный метод 3.4 (комбинация всех), суть которого состоит в последовательном применении методов 3.1–3.3 к матрице А с последующим выбором лучшего маршрута среди сформированных этими методами.
Для того чтобы можно было оценить точность приближенной методики разработана рекурсивная процедура (RecoursiveMethod), позволяющая получить точное решение задачи переборным методом. Для повышения быстродействия в процедуру внесены некоторые очевидные эвристические усовершенствования. Процедура позволила получить точное решение за приемлемое для проведения необходимых оценок время (до 5 минут на вариант размещения городов) при N<23.
Для оценки точности метода при больших значениях N (N>22) процедуру RecoursiveMethod применить нельзя, поэтому составлена процедура Rand многократного применения метода к одной и той же матрице А с различными случайными базовыми маршрутами. Процедура последовательно формирует маршруты до тех пор, пока последний лучший маршрут не повторится 5 раз подряд. Нельзя сказать, что такой способ позволяет найти самый короткий маршрут. Однако результаты работы процедуры дают интуитивную уверенность в том, что сравнение «быстрого» результата с результатом длительной работы метода имеет достаточно высокую вероятность корректности за неимением точных методов. Уверенность в этом подкреплена весьма важным выводом, который получен после обработки сотен различных матриц для N<23. Он состоит в полном совпадении результатов, полученных с использованием точной процедуры RecoursiveMethod и приближенной Rand (т. е. для данных N процедура Rand всегда находила точное решение задачи).
Скриншот интерфейса разработанной в среде Delphi 6 программы показан на .
В качестве примера на рисунке представлен кратчайший маршрут из вершины 0 в вершину 13 (N = 14) для матрицы расстояний, которая показана на рисунке 4.

Рисунок 4. Матрица расстояний
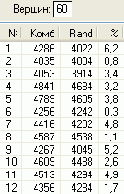
На рисунках 5-10 показаны результаты расчета маршрутов и их протяженности (Комб и Rand) для случайного расположения городов при помощи быстрой процедуры комбинированного метода и процедуры Rand. В последней колонке таблиц приведена процентная погрешность метода , которую рассчитывали по формуле 100 (Комб-Rand)/Комб, %.
 |
 |
 |
||
| Рисунок 5 | Рисунок 6 | Рисунок 7 | ||
 |
 |
 |
||
| Рисунок 8 | Рисунок 9 | Рисунок 10 |
В результате экспериментов с несколькими сотнями матриц расстояний для различных N, получены данные, которые свидетельствуют, что независимо от количества N городов погрешность метода никогда не превосходила 8% при N<101. Средняя погрешность составила 2%, что вполне приемлемо для практики.
На основании обработки многочисленных расчетных данных получена формула ориентировочной оценки быстродействия метода . Среднее время t (с) расчета на компьютере с процессором Intel 1400 кратчайшего маршрута с N городами составило 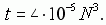
Так, для N = 100 среднее время расчета маршрута составляет 4 секунды. Для практически используемых N<31 это время не превосходит 0,1 с.